Example simulation

Before you start

Make sure you have the following:

• A cmake-based C++ project

• Proper compiler flags are set in the CMakeLists.txt file (see installation)

Configuring the environment

In this part of the tutorial, we will install the dependencies for in your cmake-based project. The dependencies are libgran, libeigen, and libtimestep.

1. If not done so already, initialize a git repository in your project root. Execute the following command:

   git init

2. The dependencies will be installed as git submodules in the deps directory. Execute the following commands:

   git submodule add https://gitlab.com/libeigen/eigen.git deps/eigen git submodule add https://github.com/egor-demidov/libgran deps/libgran git submodule add https://github.com/egor-demidov/libtimestep deps/libtimestep

3. Now, we need to configure the build system to search for header files in the installed submodules. Add the following directives to your CMakeLists.txt file:

   include_directories(deps/libtimestep/include) include_directories(deps/libgran/include) include_directories(deps/eigen)

Creating the driver program

In this part of the tutorial, we will create a driver program that will use the granular system template together with the frictional contact and Van der Waals force models to simulate a granular system.

1. If not done so already, create a C++ source file and add it as a target to your cmake project. At the top of the source file, add the following include statements:

   #include <vector> #include <iostream> #include <cmath> #include <sstream> #include <fstream> // Using Eigen for linear algebra #include <Eigen/Eigen> #include <libgran/contact_force/contact_force.h> #include <libgran/hamaker_force/hamaker_force.h> #include <libgran/granular_system/granular_system.h>

   In addition to some STL headers and libeigen, we included three libgran headers. Two of them define the force models that we want to use in this simulation, frictional contact force and Van der Waals force, and the third header defines the granular system template.

2. Now, let us "assemble" the templates that we will use and create shorter aliases for the produced types. After your includes, add the following statements:

   using contact_force_functor_t = contact_force_functor<Eigen::Vector3d, double>; // Contact force using vdw_force_functor_t = hamaker_functor<Eigen::Vector3d, double>; // Van der Waals force using binary_force_container_t = binary_force_functor_container<Eigen::Vector3d, double, contact_force_functor_t, vdw_force_functor_t>; // Binary force container using unary_force_container_t = unary_force_functor_container<Eigen::Vector3d, double>; // Unary force container (empty) using granular_system_t = granular_system<Eigen::Vector3d, double, rotational_velocity_verlet_half, rotational_step_handler, binary_force_container_t, unary_force_container_t>; // Granular system representation

   For each force template, we specified the primary field type (here Eigen::Vector3d) and real-valued scalar type ( here double). Then we specialized two container templates for two types of force models: binary_force_functor_container for binary forces and unary_force_functor_container for unary forces. Each container template accepts the primary field type, real-valued scalar type, and a variadic list of force model types as template arguments. Since we do not intend to use any unary force models in this simulation, we created an empty unary force container. Finally, we specialized the granular_system template, which accepts primary field type, real-valued scalar type, integrator type, step handler type, binary force container, and unary force container as template arguments.

3. Now we are ready to implement the main function. After the alias definitions, add the main function definition:

   int main() { // General simulation parameters const double dt = 1e-13; const double t_tot = 1.0e-7; const auto n_steps = size_t(t_tot / dt); const size_t n_dumps = 300; const size_t dump_period = n_steps / n_dumps; // General parameters const double rho = 1700.0; const double r_part = 1.4e-8; const double mass = 4.0 / 3.0 * M_PI * pow(r_part, 3.0) * rho; const double inertia = 2.0 / 5.0 * mass * pow(r_part, 2.0); // Parameters for the contact model const double k = 10000.0; const double gamma_n = 5.0e-9; const double mu = 1.0; const double phi = 1.0; const double mu_o = 0.1; const double gamma_t = 0.2 * gamma_n; const double gamma_r = 0.05 * gamma_n; const double gamma_o = 0.05 * gamma_n; // Parameters for the Van der Waals model const double A = 1.0e-20; const double h0 = 1.0e-9; /* Carry out the simulation ... */ return 0; }

   Inside the body of the main function, we declared and initialized the simulation constants. They include general parameters, such as time step size, number of time steps, number of data dumps, etc. The constants in this section also contain parameters for the force models that we are going to use. The list of parameters that each force model requires is provided in the class reference section. If M_PI is undefined, add the _USE_MATH_DEFINES compile definition.

4. Now, after the definition of constants, we can initialize the initial conditions for the simulation. We need to provide four buffers populated with initial values, each of size N, where N is the number of particles in the system. These buffers correspond to positions, translational velocities, orientations, and angular velocities respectively. Declare four corresponding std::vector's: x0, v0, theta0, and omega0:

   std::vector<Eigen::Vector3d> x0, v0, theta0, omega0;

   Build two cubes, with each side of a cube containing three particles. The cubes will have initial translational velocities directed towards each other. Add the following code snippet to your main function:

   const double x_offset = 10.0 * r_part; const double y_offset = 3.0 * r_part; for (size_t i = 0; i < 3; i ++) { auto x = double(i) * 2.0 * r_part; for (size_t j = 0; j < 3; j ++) { auto y = double(j) * 2.0 * r_part; for(size_t n = 0; n < 3; n ++) { auto z = double(n) * 2.0 * r_part; // Add particle to cube 1 x0.emplace_back(x, y, z); // Set velocity of the newly created particle v0.emplace_back(0.5, 0.0, 0.0); // Add particle to cube 2 x0.emplace_back(x + x_offset, y + y_offset, z); // Set velocity of the newly created particle v0.emplace_back(-0.5, 0.0, 0.0); } } }

   Now, set the remaining buffers - orientations and angular velocities - to zero. Add the following code to your main function:

   // Initialize the remaining buffers theta0.resize(x0.size()); omega0.resize(x0.size()); std::fill(theta0.begin(), theta0.end(), Eigen::Vector3d::Zero()); std::fill(omega0.begin(), omega0.end(), Eigen::Vector3d::Zero());

5. The next step is to create instances of the force models, force model containers, and the step handler. Add the following code to your main function:

   // Create an instance of contact force model contact_force_functor_t contact_force_model(x0.size(), k, gamma_n, k, gamma_t, mu, phi, k, gamma_r, mu_o, phi, k, gamma_o, mu_o, phi, r_part, mass, inertia, dt, Eigen::Vector3d::Zero(), 0.0); // Create an instance of Hamaker model vdw_force_functor_t hamaker_model(A, h0, r_part, mass, Eigen::Vector3d::Zero(), 0.0); // Create an instance of binary force container binary_force_container_t binary_force_functors{contact_force_model, hamaker_model}; // Create an instance of unary force container (empty) unary_force_container_t unary_force_functors; // Create an instance of step_handler rotational_step_handler<std::vector<Eigen::Vector3d>, Eigen::Vector3d> step_handler_instance;

   Now, initialize the granular system object by passing references to force model containers and the step handler to the constructor:

   granular_system_t system(x0, v0, theta0, omega0, 0.0, Eigen::Vector3d::Zero(), 0.0, step_handler_instance, binary_force_functors, unary_force_functors);

6. Now, all that is left to do is time stepping. Add the following loop that performs n_steps iterations and advances the granular system by time step dt at each iteration:

   for (size_t n = 0; n < n_steps; n ++) { if (n % dump_period == 0) { /* TODO: add some code to dump data */ } system.do_step(dt); }

   To advance the system by one time step of size dt, we simply need to call the do_step(dt) method of the granular system object.

7. If you run the program now, the simulation will be performed but no output will be produced. We need to add some code to write out the state of the system periodically. Above your main function, add a new declaration:

   void dump_particle_positions(std::string const & dir, size_t count, std::vector<Eigen::Vector3d> const & x, double r_part) { std::stringstream out_file_name; out_file_name << dir << "/particles_" << count << ".csv"; std::ofstream ofs(out_file_name.str()); if (!ofs.good()) { std::cerr << "Unable to create a dump file at " << out_file_name.str() << std::endl; exit(EXIT_FAILURE); } ofs << "x, y, z\n"; for (auto const & point : x) { ofs << point[0] / r_part << ", " << point[1] / r_part << ", " << point[2] / r_part << "\n"; } }

   Now back in your integration loop, where you left space for data dumping code, add:

   dump_particle_positions("run", n / dump_period, system.get_x(), r_part);

   Now, create a directory named run in the same directory as the executable and run the simulation. You should see the run directory get populated with 300 .csv files, each containing the coordinates of all particles at the corresponding time step.

Visualizing the results

In this section of the tutorial, we will set up a visualization of the granular system using the .csv files generated at the previous step.

1. Generated data files can be visualized using ParaView. To create a visualization, open the files in ParaView. Press File->Open and navigate to the directory with generated data files. ParaView will automatically recognize sequentially numbered files as a time series:

   

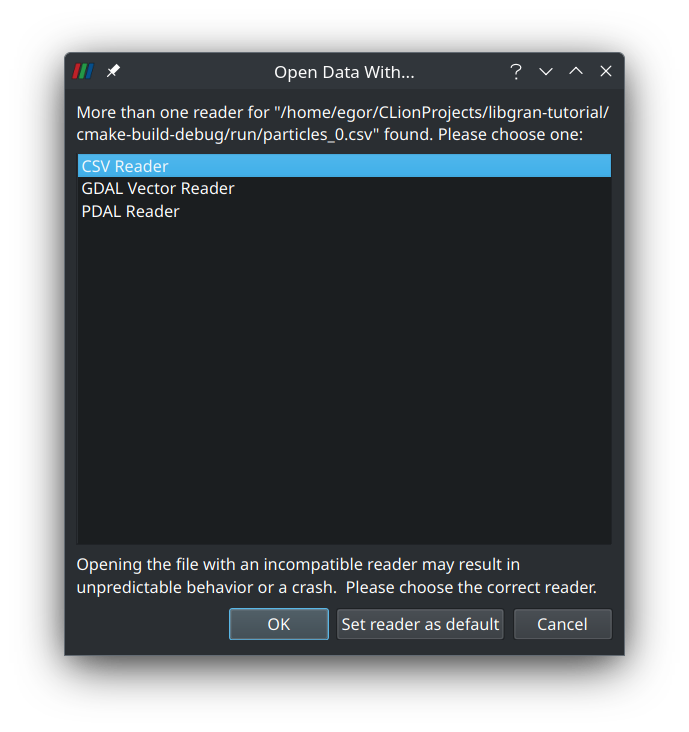
2. Select the entry and press OK. ParaView will ask to select the appropriate data reader. Select the CSV reader and press OK:

   

3. ParaView will load the data as a table. Press the green Apply button in the left panel. A table previewing the data should appear on the right side of the screen. This preview can be closed.

   

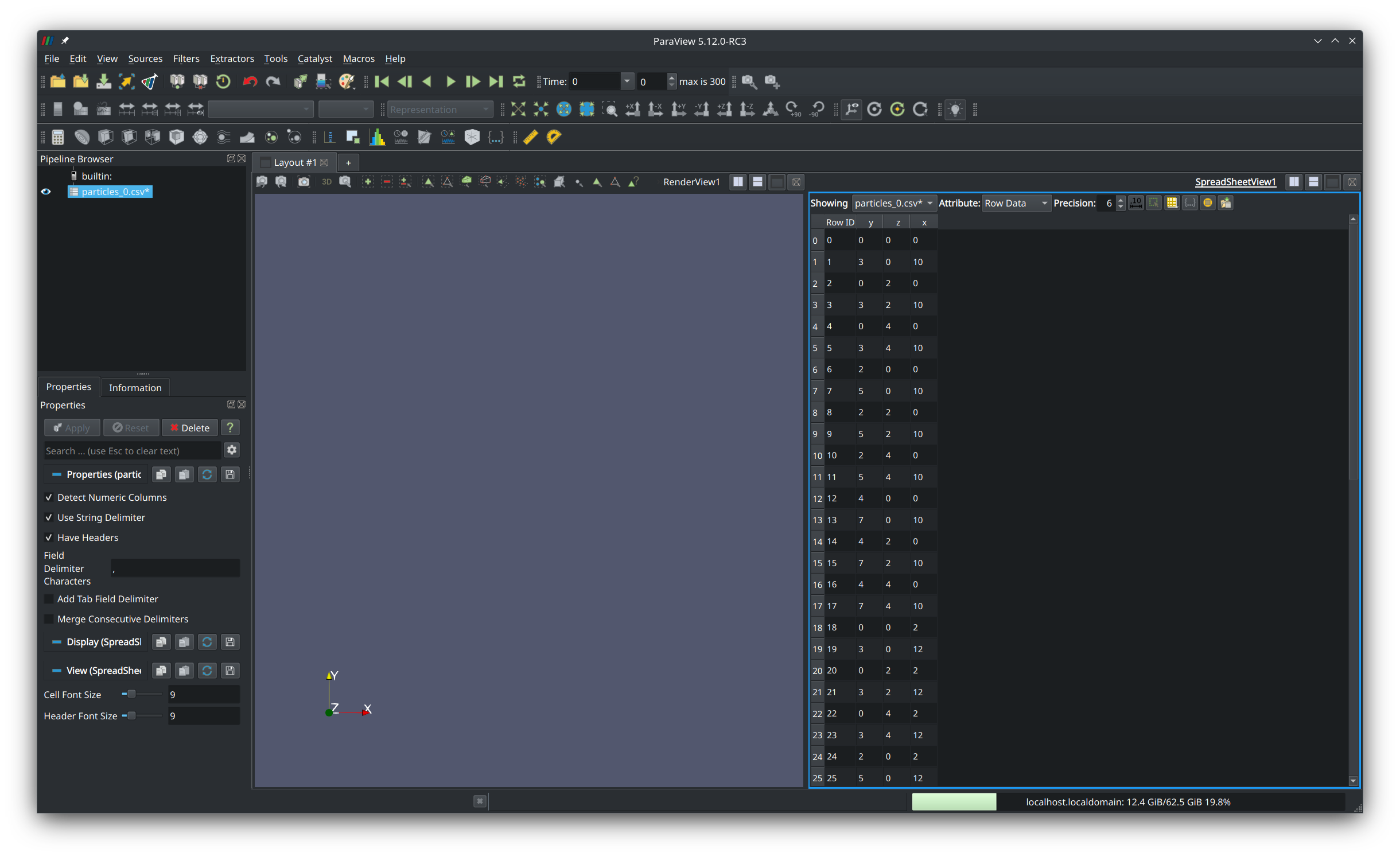
4. Now, we need to tell ParaView to interpret the rows in the loaded table as x-y-z points. Select the loaded data set in the left panel and got to Filters->Seacrh. Start typing table to points and select the corresponding filter when it appears among search results.

   

5. Now in the left panel there should be a filter that is a child of the table. Click on it and in the dropdowns, select x column, y column, and z column to be x, y, and z respectively.

   

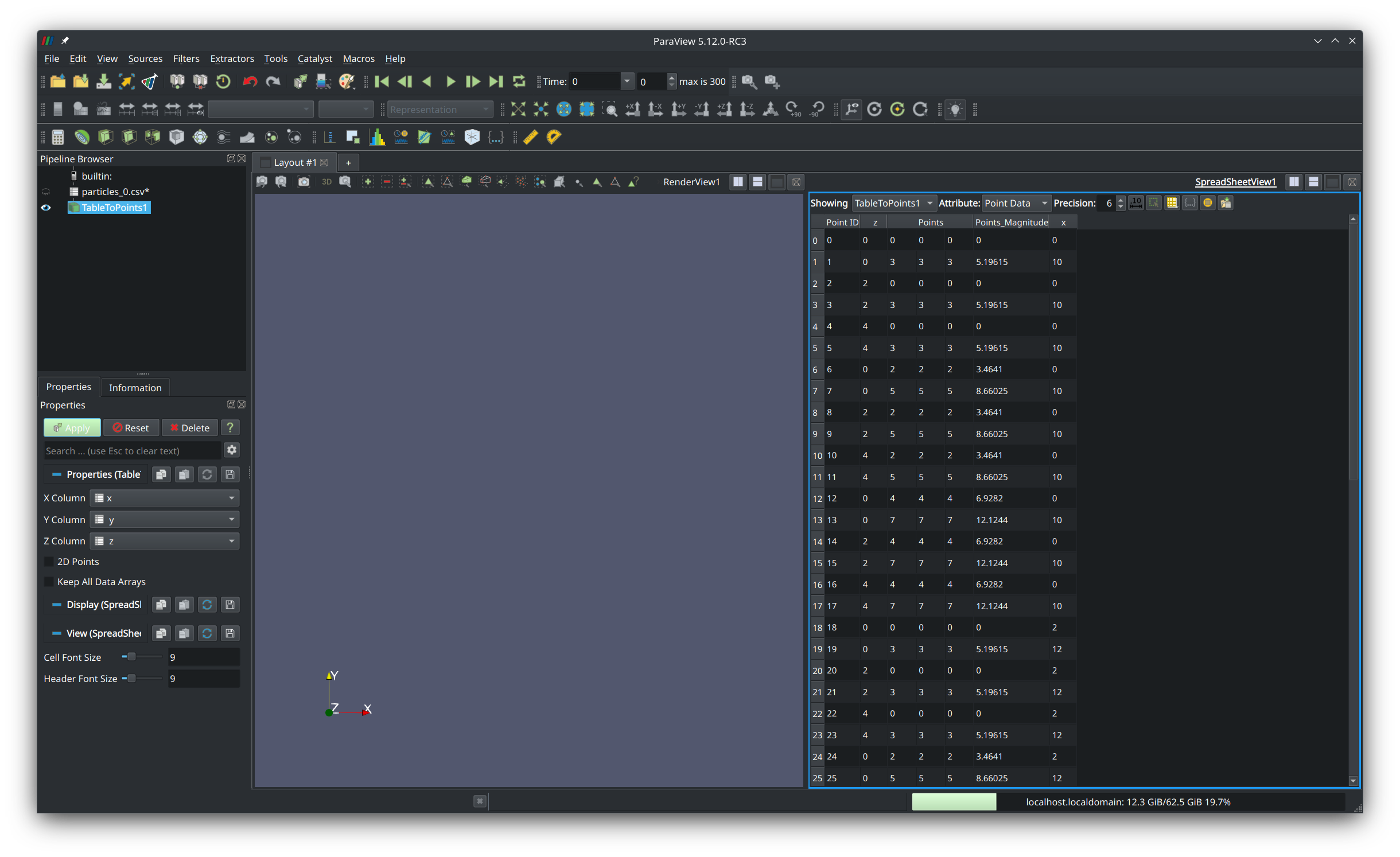
6. Press the green Apply button. With the filter selected in the left panel, click the Glyph button in the ribbon. In the left panel, set Glyph Type to sphere, scale array and orientation array to none, scale factor to 2, and Glyph Mode to all points. Click the green Apply button. Cubes made up of spherical particles should appear: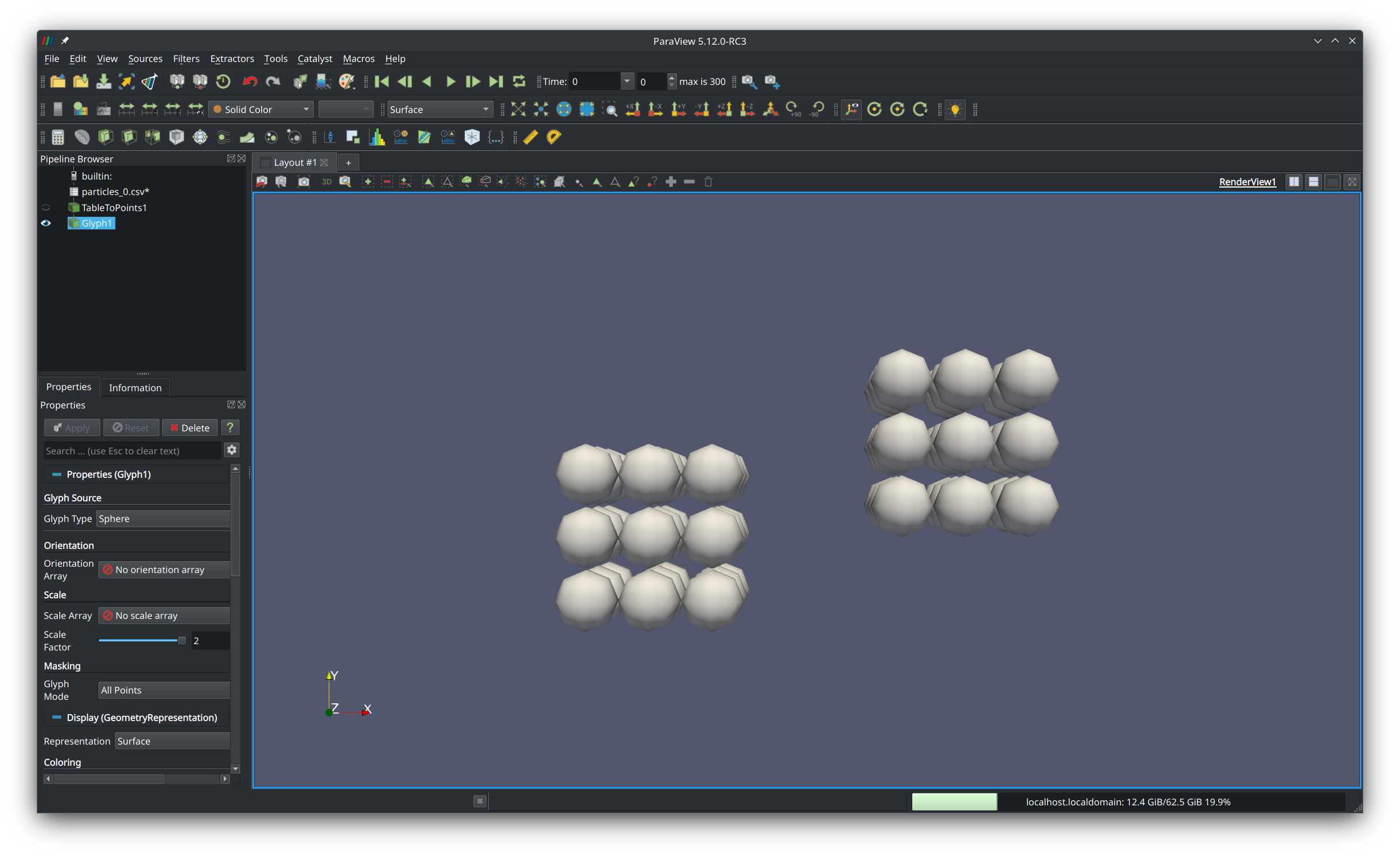

   

7. In the top ribbon, you can see that the current frame is 0 out of 300. You can press the green play button to preview the animation, or directly type in 300 in the text box to jump to the last frame. If you do so, you will see that at the end of the simulation, the cubes had collided and are now stuck together.

   

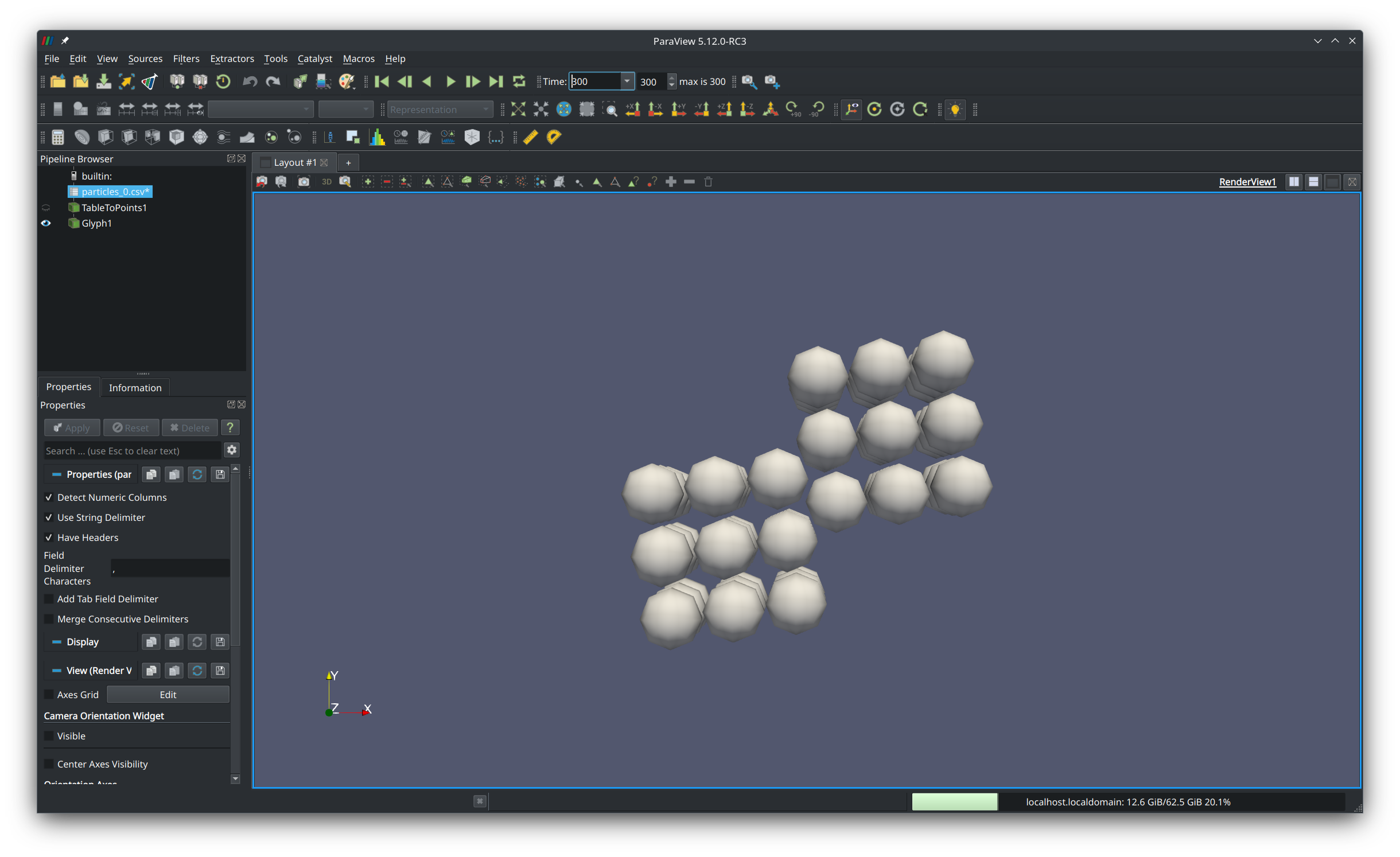
What you've learned

You have learned how to:

• Initialize a simulation using built-in force models

• Run a simulation and output the results to a .csv file

• Create a visualization using ParaView

Complete source file